Python :
FreeFEM++ :
LATEX :
EDUCATION
2020–2023 PhD, LMBP, Université Clermont Auvergne, Clermont-Ferrand, "Analysis, control, and simulation for non-Newtonian fluid flows", supervised by Laurent Chupin and Nicolae Cîndea
2019–2020 Preparatory class for the agrégation exam, Université Claude Bernard Lyon 1, Villeurbanne,
2019–2020 M.Sc., Université de Franche-Comté, Besançon, Scientific computing
2018–2019 M.Sc., Université Claude Bernard Lyon 1 and ENS Lyon, Lyon, Partial Differential Equations
2016–2018 M.Sc., Université Franche-Comté, Besançon, Variational methods for elliptic PDEs, Fourier analysis
2013–2016 B.Sc., Université de Franche-Comté, Besançon
PhD Thesis
Title : Analysis, control, and simulation for non-Newtonian fluid flows
Supervisors : Laurent Chupin, Nicolae Cîndea
Description : The first objective of this thesis is to show the existence of solutions for a class of incompressible viscous fluids whose flows are characterized by a viscosity that can vary as a function of the velocity field. In particular, the studied equations can be seen as Navier-Stokes equations with an additional nonlinearity (like a p-laplacian for example). Then, we are interested in the controllability of the solutions of such equations, in exact or optimal control depending on the problem considered. Finally, we illustrate the results through numerical analysis and simulations for these models.
Master Thesis
Title : About some kind of decay for the energy of Leray solutions to the Navier-Stokes equations on the whole space
Supervisor : Lorenzo Brandolese
Description : The objective of this master thesis was to characterize the long-time polynomial decay of energy for Leray solutions to the Navier-Stokes equations for an incompressible viscous fluid when the initial velocity field belongs to L2σ. The method used micro-local analysis tools, including characterization of the heat kernel as belonging to suitable homogeneous Besov spaces.
Master Thesis
Title : Two solutions for a quasilinear problem
Supervisor : Louis Jeanjean
Description : The objective of this master thesis was to show the existence of several nontrivial solutions for the quasilinear elliptic equation:
in the homogeneous Dirichlet setting. The nonexistence of such a solution by a blow-up method for certain values of λ was established, as well as the existence of a solution in the case of a sublinear growth of f, using Palais-Smale sequences and after showing that the functional associated to the solution possessed a mountain pass geometry.
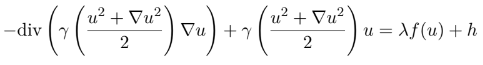
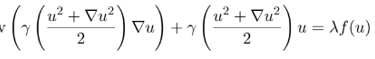
LANGUAGES
French : Native
English : C1
